4.8 – Vapour Pressure

4.8.0 – Learning Objectives

By the end of this section you should be able to:

  1. Understand the concept of vapour pressure.
  2. Use the Antoine equation.
  3. Know when you should use Raoult’s law.
  4. Know when you should use Henry’s law.
  5. Distinguish between the different types of saturation’s and humidity’s.

4.8.1 – Introduction

Vapour pressure is the pressure a vapour exerts with its solid or liquid at a given temperature at equilibrium. This means that vapour pressure is a good indication of a liquid’s evaporation rate or a solid’s sublimation rate.

4.8.2 – Vapour Pressure

As you can see in the figure bellow, vapour pressure is at equilibrium. This means that there is as much vapour being produced from evaporation as vapour being consumed due to condensation. The magnitude of the vapour pressure tells you how volatile the liquid is. The higher the vapour pressure, the higher the volatility.

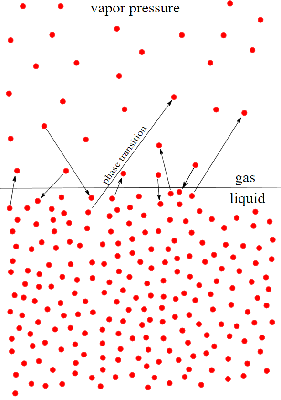
Attribution: By HellTchi (Own work) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons

4.8.3 – Antoine equation

The Antoine equation is simple yet crucial equation the relates vapour pressure and temperature. The equation is:

\[\log_{10} p^* = A - \frac{B}{T + C}\]

Where A, B, and C are constants that can be found in tables and

\[p^* = \text{Vapour Pressure}\]
\[T = \text{Temperature}\]

4.8.4 – Raoult’s Law and Henry’s Law

Raoult’s law and Henry’s law provide us with a relationship between the partial pressure of a substance, \(P_A\), in the gas phase and the mole fraction of the same substance, \(x_A\), in the liquid phase. Raoult’s law is generally valid when \(x_A\) is close to 1, which means the liquid is almost pure A. Henry’s law is generally valid when solutions of \(x_A\) are close to 0.

The expression for Raoult’s law is:

\[p_A \equiv y_A P = x_A p_A^* (T)\]

where

\[p_a = \text{Is the partial pressure of substance A}\]
\[y_A = \text{Is the mole fraction of substance A in the gas phase}\]
\[P = \text{Is the pressure of the system}\]
\[x_A = \text{Is the mole fraction of substance A in the liquid phase}\]
\[p_A^* (T) = \text{Is the vapour pressure of pure liquid A at temperature T}\]

The expression for Henry’s law is:

\[p_A \equiv y_A P = x_A H_A (T)\]

where

\[p_a = \text{Is the partial pressure of substance A}\]
\[y_A = \text{Is the mole fraction of substance A in the gas phase}\]
\[P = \text{Is the pressure of the system}\]
\[x_A = \text{Is the mole fraction of substance A in the liquid phase}\]
\[H_A (T) = \text{Is the the Henry's law constant for A in a specific solvent}\]

4.8.5 – Saturation and Humidity

The term saturation refers to any gas-vapour system. Humidity refers specifically to an air-water system. There are four main types of saturation and humidity:

Relative Saturation (Relative Humidity):

\[s_r (h_r) = \frac{p_i}{p^*_i (T)} \times 100 \text{%}\]

where

\[p_i = \text{The partial pressure of species i}\]
\[p^*_i (T) = \text{The vapour pressure of species i}\]

Molal Saturation (Molal Humidity):

\[s_m (h_m) = \frac{p_i}{P - p_i}\]

where

\[p_i = \text{The partial pressure of species i}\]
\[P = \text{The total pressure of the system}\]

Absolute Saturation (Absolute Humidity):

\[s_a (h_a) = \frac{p_i M_i}{(P - p_i) M_{dry}}\]

where

\[p_i = \text{The partial pressure of species i}\]
\[P = \text{The total pressure of the system}\]
\[MW_i = \text{The molecular weight of species i}\]
\[MW_{dry} = \text{The average molecular weight of all of the none vapour gas of the system}\]

Percentage Saturation (Percentage Humidity):

\[s_p (h_p) = \frac{s_m}{s^*_m} \times 100 \text{%} = \frac{\frac{p_i}{P - p_i}}{\frac{p^*_i}{P - p^*_i}} \times 100 \text{%}\]

where

\[p_i = \text{The partial pressure of species i}\]
\[p^*_i = \text{The vapour pressure of species i}\]
\[P = \text{The total pressure of the system}\]

Each one of these different types of saturation and humidity’s are useful in different scenarios.

4.8.6 – Problem Statement

Problem 1

Question

Humid air at \(60^{\circ} C\), 1 atm, and 73 % relative humidity is fed into a unit operation at a rate of \(500 \space m^3 / h\). The vapor pressure of water at 1 atm and \(60^{\circ} C\) is \(p^*_{H_2 0} = 19,920 \space Kpa\). Determine

  1. the molar flow rates of water, dry air, and oxygen, assuming oxygen makes up 21% of dry air.
  2. the molal humidity, absolute humidity, and percentage humidity of the air.

Answer

a) the molar flow rates of water, dry air, and oxygen, assuming oxygen makes up 21% of dry air

First we must determine the partial pressure of the water.

\[p_{H_2 O} = h_r \cdot p^*_{H_2 0} = (0.73) \cdot 19,920 = 14,540 \space Pa\]

Then using Raoult’s Law, we can fine the vapour mole fraction of the water

\[y_{H_2 O} = \frac{p_{H_2 O}}{P} = \frac{14,540 \space Pa}{101,300 \space Pa} = 0.1435 \space \frac{mol \space H_2 O}{mol}\]

Assuming the humid air behaves ideally, we can use the ideal gas law to solve for the molar flow rate of the wet air

\[\dot{n}_{total} = \frac{P \dot{V}}{R T} = \frac{ \big(101,300 \space Pa \big) \big(500 \space \frac{m^3}{h} \big)}{\big(8.314 \frac{ m^3 \cdot Pa}{mol \cdot K} \big) \big(333.15 \space K \big)} = 18,300 \space \frac{mol}{h}\]

Since we know the mole fraction of the water is

\[y_{H_2 O} = 0.1435 \space \frac{mol \space H_2 O}{mol}\]

then we can solve the mole fraction of the dry hair by

\[y_{dry} = y_{wet} - y_{H_2 O} = (1 - 0.1435) \space \frac{mol \space H_2 O}{mol} = 0.8565 \space \frac{mol \space H_2 O}{mol}\]

Since the mole fraction of oxygen in dry air is

\[y_{oxy} = 0.21\]

We can finally solve for the molar flow rate of water, dry air, and oxygen.

\[\dot{n}_{H_2 O} = \dot{n}_{total} \cdot y_{H_2 O} = \big( 18,300 \space \frac{mol}{h} \big) \cdot \big(0.1435 \space \frac{mol \space H_2 O}{mol} \big) = 2.626 \space \frac{kmol}{h}\]
\[\dot{n}_{dry} = \dot{n}_{total} \cdot y_{dry} = \big( 18,300 \space \frac{mol}{h} \big) \cdot \big(0.8565 \space \frac{mol \space H_2 O}{mol} \big) = 15.67 \space \frac{kmol}{h}\]
\[\dot{n}_{oxy} = \dot{n}_{total} \cdot y_{oxy} = \big( 15,700 \space \frac{mol}{h} \big) \cdot \big(0.21 \space \frac{mol \space H_2 O}{mol} \big) = 3.291 \space \frac{kmol}{h}\]
b) the molal humidity, absolute humidity, and percentage humidity of the air

We have already solved for the partial pressure of the water vapor so solving for the molal humidity

\[h_m = \frac{p_{H_2 O}}{P - p_{H_2 O}} = \frac{14,540 \space Pa}{101,300 \space Pa - 14,540 \space Pa} = 0.1675 \frac{mol \space H_2 O}{mol \space dry}\]

The MW is 18.00 g/mol while the average MW of dry air is 28.9 g/mol. With that knowledge, we can solve for absolute humidity

\[h_a = \frac{p_{H_2 O} \cdot MW_{H_2 O}}{(P - p_{H_2 O}) MW_{dry}} = \frac{(14,540 \space Pa)(18.00 \space g/mol)}{(101,300 \space Pa - 14,540 \space Pa)(28.9 \space g/mol)} = 0.104 \frac{kg \space H_2 O}{kg \space dry}\]

Finally, to find the percentage humidity we must

\[h_p = \frac{\frac{p_{H_2 O}}{P - p_{H_2 O}}}{\frac{p^*_{H_2 O}}{P - p^*_{H_2 O}}} \times 100 \text{%} = \frac{\frac{14,540 \space Pa}{101,300 \space Pa - 14,540 \space Pa}}{\frac{19,920 \space Pa}{101,300 \space Pa - 19,920 \space Pa}} \times 100 \text{%} = 68.5 \text{%}\]

Problem 2

Question

Find the temperature at which the vapour pressure of water is \(6,000 \space Pa\) where

\[A = 10.116\]
\[B = 1687.537\]
\[C = -42.98\]

Answer

Using Antione’s equation

\[\log_{10} p^* = A - \frac{B}{T + C}\]

we can plug in the values and solve for \(p^*\).

\[\log_{10}(6000) = 10.116 - \frac{1687.537}{T + (-42.98)}\]
\[T = \frac{1687.537}{10.116 - \log_{10}(6000)} + 42.98\]
\[T = 308.3 \space K\]

Answer Using Python

Typically, Antoine’s constants are not given to you and you will have to look them up in a table. This may be tedious especially for chemicals less common than water. We can use the thermo library, show in section 4.3, to help us find the answer.

In [1]:

!pip install thermo --user

Requirement already satisfied: thermo in c:\users\said zaid-alkailani\appdata\roaming\python\python36\site-packages
Requirement already satisfied: fluids in c:\users\said zaid-alkailani\appdata\roaming\python\python36\site-packages (from thermo)
Requirement already satisfied: scipy in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from thermo)
Requirement already satisfied: pandas in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from thermo)
Requirement already satisfied: coolprop in c:\users\said zaid-alkailani\appdata\roaming\python\python36\site-packages (from thermo)
Requirement already satisfied: python-dateutil>=2 in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from pandas->thermo)
Requirement already satisfied: pytz>=2011k in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from pandas->thermo)
Requirement already satisfied: numpy>=1.7.0 in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from pandas->thermo)
Requirement already satisfied: six>=1.5 in c:\users\said zaid-alkailani\anaconda3\lib\site-packages (from python-dateutil>=2->pandas->thermo)

In [2]:

from thermo.chemical import Chemical
T = Chemical('water').VaporPressure.solve_prop(6000)
print("The temperature at which the vapour pressure is 6,000 Pa is", T, "K")

The temperature at which the vapour pressure is 6,000 Pa is 309.32672149807246 K

Citation

Caleb Bell (2016). thermo: Chemical properties component of Chemical Engineering Design Library (ChEDL) https://github.com/CalebBell/thermo.

In [ ]: